Поле из треугольников, смятое в кристаллическое море. Мяч с поверхностью, изрезанной щупальцами лабиринтных коридоров. Прибой из аккуратного кирпичного узора. Хвосты морских коньков… Поток таких романтических ассоциаций сразу же приходит на ум, едва начинаешь рассматривать спидрон — эту изящную математическую выдумку.
Даниэль Эрдели (Dániel Erdély), венгерский художник и дизайнер, придумал спидроны в 1970-х годах. Началось всё с того, что он нарисовал фигуру в виде двух "завитков", собранных из треугольников. Отдалённо эта структура напоминает рукава или бар галактики, но стали ли источником вдохновения астрономические наблюдения — неизвестно.
).Поле из треугольников, смятое в кристаллическое море. Мяч с поверхностью, изрезанной щупальцами лабиринтных коридоров. Прибой из аккуратного кирпичного узора. Хвосты морских коньков… Поток таких романтических ассоциаций сразу же приходит на ум, едва начинаешь рассматривать спидрон — эту изящную математическую выдумку.
Даниэль Эрдели (Dániel Erdély), венгерский художник и дизайнер, придумал спидроны в 1970-х годах. Началось всё с того, что он нарисовал фигуру в виде двух "завитков", собранных из треугольников. Отдалённо эта структура напоминает рукава или бар галактики, но стали ли источником вдохновения астрономические наблюдения — неизвестно.
Каким образом Эрдели создал это изображение?
Спидрон состоит из равнобедренных и равносторонних треугольников, расположенных определённым образом. Для начала нужен равнобедренный треугольник с углом 120 градусов.
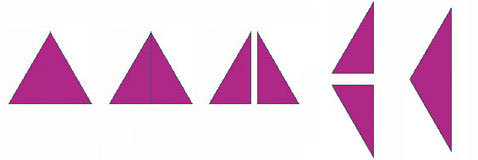 |

Сделать такой треугольник можно очень просто, например, из равностороннего. В равностороннем треугольнике надо провести перпендикуляр от вершины до одной из сторон (высота), затем "разрезать" его по этой линии и соединить меньшими сторонами. В результате получится нужный треугольник, у которого один угол равен 120 градусам, а два других — по 30. |
Теперь можно заняться собственно спидроном.
Берём наш треугольник и на одной из его бóльших сторон пририсовываем равносторонний треугольник.
 |

Так вот. |
А на одной стороне равностороннего "делаем" равнобедренный, подобный предыдущему. Для этого у равностороннего нужно отметить центр и отрезками соединить его с вершинами — получатся три одинаковых равнобедренных треугольника (у каждого из них будет угол 120 градусов). После этого надо сделать "отражение" одного из них так, чтобы он соприкасался со стороной равностороннего.
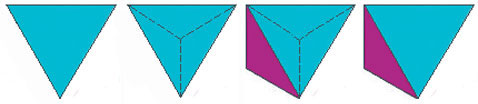 |

Вот так. |
Потом на одной из сторон этого "отражённого" треугольника снова строим равносторонний (очевидно, он будет меньше предыдущего равностороннего). И так далее — в общем-то, до бесконечности (или пока не надоест).
 |

Получаем такую загогулину. Но это ещё не всё. |
А теперь нужно сделать копию этого "рукава" и прилепить её к уже имеющемуся.
 |

Вот так и выглядел первый спидрон. Может, он не был цветным, но это уже совсем не важно. Теперь, кстати, понятно, почему фигура так зовётся — это действительно "смесь" спирали (spiral) и граней (греческое hedra — "грань") (иллюстрация Dániel Erdély). |
У спидрона Эрдели обнаружил интересное свойство: площадь любого равностороннего треугольника в любом рукаве равна сумме площадей всех последующих меньших треугольников. Другими словами, в равносторонний треугольник можно вписать все остальные, которые строились после него.
Однако вскоре он открыл более впечатляющие особенности спидронов. Если вырезать эти фигуры из бумаги и сгибать их по граням, то они могут складываться наподобие мехов аккордеона. Интересно и то, что множество таких, теперь уже трёхмерных, спидронов можно использовать для создания самых разнообразных рельефных поверхностей.
 |

Вот такое бушующее "море спидронов". Как ни странно, но подобная конструкция скоро может оказаться ценным инженерным решением (иллюстрация Pelletier, Erdély, van Ballegooijen, Buhler Allen). |
Более того, оказалось, что если сделать небольшое отверстие в месте соединения спидронов, то их движение происходит намного проще. А это значит, что рельеф поверхности, собранной из них, может легко изменяться.
В 1979 году Эрдели решился показать изобретение своему преподавателю Эрно Рубику (Ernö Rubik) — тому самому, что придумал небезызвестный кубик. Эрно очень удивился и сказал, что никогда не видел ничего подобного. После столь авторитетной оценки Эрдели, конечно, очень обрадовался и решил продолжить работу с геометрией спидронов.
 |

Варьируя пропорции треугольников, составляющих спидрон, можно до неузнаваемости изменить рельеф поверхности (иллюстрация с сайта szinhaz.hu). |
Чуть позже о спидронах узнал Марк Пельтье (Marc Pelletier), один из основателей компании Zome System, занимающейся созданием различных геометрических моделей для школьных занятий. Он тоже пришёл в восторг от увиденного и сказал, что эти фигуры можно использовать для всевозможных скульптурных конструкций.
 |


Спидроны и конструкции из них стали центральной темой одного из недавних выпусков журнала Science News (иллюстрация с сайта sciencenews.org). | |
 |
Впрочем, в процессе сотрудничества Эрдели с некоторыми художниками и математиками выяснилось, что эти фигуры стоит использовать не только для построения художественных объектов. Им можно найти достойное применение при разработке некоторых регулируемых динамических конструкций.
Ведь если к "спидроновому рельефу" приложить усилие, то спидроны начнут скручиваться, из-за чего механическое напряжение поверхности усилится, и поверхность будет как бы пружинить. Поэтому такие структуры можно использовать, к примеру, в качестве амортизаторов, для изготовления шумопоглощающих покрытий или, скажем, для создания тонких, но не ломающихся солнечных панелей.
Вдобавок ко всему Эрдели уверен, что его изобретение можно применять и в производстве игрушек, а также в качестве строительных материалов. Ну-ну…
 |

Несть числа милым математическим забавам со спидронами (иллюстрация с сайта spidron.hu). |
Почему-то художник не очень торопился рассказывать научному миру о своих разработках. Но однажды он познакомился с исследовательницей кристаллов Кристианой Григореску (Cristiana Grigorescu), по совету которой в 1998 году выступил на международной конференции по выращиванию кристаллов, где и поведал о спидронах.
 |

Один из вариантов использования спидронов — кафельная плитка. Почему бы и нет? (фото с сайта spidron.hu). |
Прошло ещё пять лет, и Лайош Силаши (Lajos Szilassi), математик из венгерского университета Сегеда, (
Szegedi Tudományegyetem) подготовил первое обстоятельное математическое описание систем из спидронов и точно определил возможные особенности их движения.
Со временем спидроны стали всё больше интересовать учёных — оказалось, что эти фигуры могут дать немало пищи для научного ума.
 |

Сборка крупномасштабной фигуры, основанной на спидронах, временами становилась очень непростой головоломкой (фото с сайта spidron.hu). |
И не только для научного: всё больше скульпторов, художников, инженеров хотят использовать спидронные конструкции в своей работе. Так что остаётся ждать, когда начнут поступать коммерческие предложения, а эти закрученные штуки найдут широкое применение. Вероятно, рано или поздно это произойдёт — ведь детали на их основе смотрятся на редкость симпатично.


Комментарии:
Нет комментариев. Почему бы Вам не оставить свой?
Для того чтобы оставить комментарий зарегистрируйтесь и войдите на сайт под своим именем.
Если Вы уже регистрировались то просто войдите на сайт под своим именем.